本文整理自 Luca Cardelli, Type Systems 的第六章内容。欢迎 star 和 follow。

子类型(Subtyping)

具有类型的面向对象编程语言有着非常有趣且复杂的类型系统。不同的面向对象语言中有着不同的特征，但其中有一个特征几乎普遍存在，即子类型(Subtyping)。子类型直观地刻画了类型之间的包含关系，所谓类型可以被视为值的集合。某个类型的元素也可以被视为其任何超类的元素，引入子类型后，编程语言就允许值(对象)在许多类型不同的上下文中灵活使用。

在考虑子类型关系时，通常会添加一个新的断言 ，表示 是 的子类型(表27)。其语义为 中的任何元素都是 的元素，或者更确切地说， 类型的程序也是 类型的程序。

具有子类型的最简单的类型系统之一是一种对 的扩展，标记为为 。 其在 的基础上添加了一种称为 的类型，它是所有类型的超类型。 现有的类型规则也保持不变。子类型断言是独立公理化的，并添加了一个称为升级(subsumption)的类型规则，用于将类型断言与子类型断言相连接。

表27. 子类型断言

升级规则表明，如果一个项具有类型 ，而 是 的子类型，那么该项也具有类型 。子类型的性质非常类似于集合的包含关系。

表28中的子类型关系被定义为反射性(reflexive)和传递性(transitive)关系，并具有一个称为 的最大类型。这个类型是所有良类型的项的类型。

函数类型的子类型关系规定，如果 是 的子类型，且 是 的子类型，则 是 的子类型。请注意，函数参数的包含是逆变(contravariant)的，而函数结果的包含是协变的(covariant)。简单的推理就可以论证这一点。类型为 的函数 接受类型 的元素；显然它也接受任何 的子类型 的元素。同样的函数 返回类型为 的元素；显然它返回属于 的任何超类型 的元素。因此，类型为 的任何函数 ，也可以接受类型为 的参数并返回类型为 的结果，因此也具有类型 。 我们因此可以说 是 的子类型。

表28. F1 的附加规则

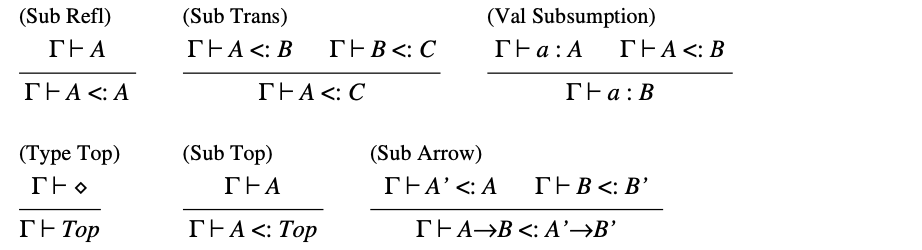
可以在基本类型上添加特定的子类型规则，比如 [19]。

我们考虑的所有作为 的扩展结构类型都可以采用简单的子类型规则；因此，这些结构类型也可以添加到 中(表29)。通常，我们需要为每个类型构造器添加一个子类型规则，确保子类型规则与升级规则可以一起工作。对于积类型和联合类型，子类型规则会作用于每个分量上(component-wise)。对于记录和变体，子类型规则和长度有关(length-wise)：更长的记录类型是更短的记录类型的子类型(子类型规则作用时可能会丢失附加的字段)，而更短的变体类型则是更长变体类型的子类型(通过子类型规则可以引入更多的情况)。例如，

则有，

引用类型没有任何子类型规则：只有当 时， 才成立。这个严格的规则是必要的，因为引用既可以读取也可以写入，因此在行为上既是协变的也是逆变的。出于相同的原因，数组类型也没有子类型规则。

表29. F1 扩展的附加规则

相比于 类型系统，在考虑递归类型时， 需要对环境的结构进行更改。这一次，我们必须向环境中添加约束变量(bounded variable)(表30)。由 绑定的变量对应于我们旧的无约束变量。对于递归类型(表31)的子类型规则(Sub Rec)的合理性的严谨论证并不简单，但却是符合直觉的。要检查 是否成立，我们可以假设 ，然后检查 ；当在协变上下文中找到 和 在 和 中的匹配出现时，可以利用这个假设进行证明。

表30. 约束变量的环境

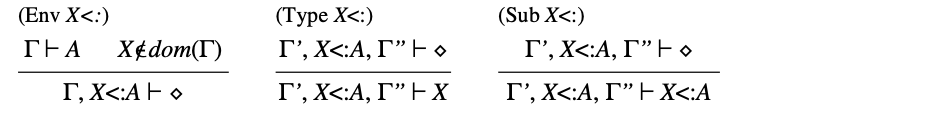
表31. 递归类型的子类型

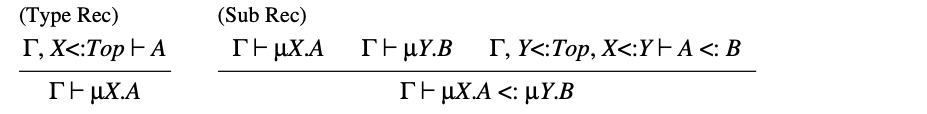
环境中的约束变量(bounded variable) 也是 子类型扩展的基础，这将产生一个称为 的系统(表32)。在这个系统中，项 表示一个程序 ，其参数为类型变量 ，该变量代表 的任意子类型。这是 的泛化，因为 项 可以表示为 。与项 对应的是形如 的约束类型量词(bounded type quantifiers)。

表32. F2 的语法

类型和项的作用域与 类型和项的作用域定义类似，只是 在 中绑定 ，但不在 中绑定 。

的类型规则包括大部分 的类型规则,即，，，，，，，，，，和，以及变量的规则，即，和，以及表33中列出的多态的规则。

表33. 约束全称量词(bounded universal quantifiers)的规则

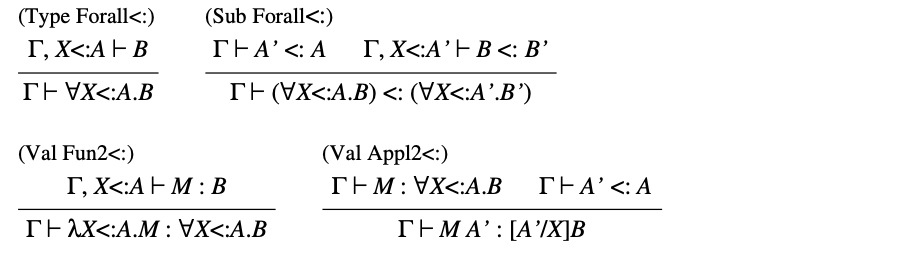
相比于 ，我们不需要向 添加其他类型构造，因为所有常见类型都可以被已有的构造表示(除了递归)。此外，事实证明， 中使用的编码也满足了子类型规则的需要。例如，可以对存在类型进行编码，以满足表34中描述的规则。类型 表示部分抽象类型(partially abstract type)，其表示类型 不完全已知，但一定是 的子类型。这种部分抽象在一些基于子类型的语言中有用到(例如，在 Modula-3 中)。

表34. 约束存在量词(bounded existential quantifiers)的规则

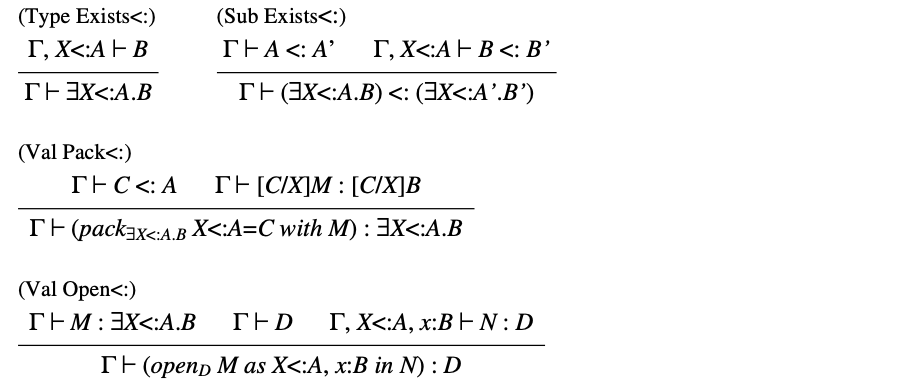
为了在 中满足预期的子类型规则，需要对 中的记类型录和变体类型进行编码，这需要一些复杂的工作，可以参考[6]。

参考

[6] Cardelli, L., Extensible records in a pure calculus of subtyping. In Theoretical Aspects of Object-Oriented Programming, C.A. Gunter and J.C. Mitchell, ed. MIT Press. 373-425. 1994. [19] Mitchell, J.C., Coercion and type inference. Proc. 11th Annual ACM Symposium on Principles of Programming Languages, 175-185. 1984.